60. Площадь многоугольника
Заданы
координаты n последовательных вершин
многоугольника. Определить его площадь.
Вход. Первая строка
содержит количество вершин многоугольника n
(3 ≤ n ≤ 50000). В
следующих n строках заданы координаты
его последовательных вершин xi, yi (-1000 ≤ xi,
yi ≤ 1000).
Выход. Вывести площадь
многоугольника с тремя десятичными знаками.
|
Пример входа |
Пример выхода |
|
3 0 0 0 2 2 0 |
2.000 |
РЕШЕНИЕ
геометрия
Анализ алгоритма
Пусть А1(x1, y1), А2(x2,
y2), …, Аn(xn,
yn) – координаты вершин простого
(без самопересечений) многоугольника, заданные в порядке его обхода по или
против часовой стрелки. Тогда его площадь вычисляется по формуле трапеций:
S = ![]()
где Аn+1(xn+1, yn+1) = А1(x1, y1). Значение суммы следует брать по модулю, так как оно
может быть как положительным, так и отрицательным в зависимости от направления
обхода многоугольника.
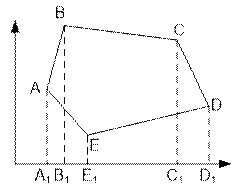
Площадь трапеции
положительна при xi+1 > xi и отрицательна при xi > xi+1.
Площадь
многоугольника ABCDE равна
![]() +
+ ![]() +
+ ![]() –
– ![]() –
– ![]()
Площадь
многоугольника можно найти по формуле Сюрвейера (Surveyor):
S =  =
= 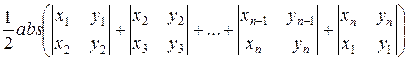
Пусть О(0, 0) –
центр координат. Тогда площадь многоугольника равна сумме площадей
треугольников OA1A2, OA2A3, OA3A4, … , OAnA1. Если
треугольник ориентирован против часовой стрелки, то его площадь положительна.
Если против – то отрицательна. Площадь треугольника OAiA i+1 равна
 =
= 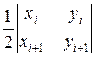
Реализация алгоритма
Координаты точек
храним в векторах x и y. То есть координаты i-ой
точки будут содержаться в (x[i], y[i]).
#define MAX 1002
int x[MAX], y[MAX];
Функция findArea
вычисляет площадь многоугольника по выше приведенной формуле трапеций.
double findArea(int
*x, int *y)
{
double s = 0;
x[n] = x[0]; y[n] = y[0];
for(int i = 0; i <
n; i++)
s += (y[i+1] +
y[i]) * (x[i+1] - x[i]) / 2.0;
return (s < 0) ?
-s : s;
}
Основная часть
программы. Читаем
входные данные.
scanf("%d",&n);
for(i = 0; i < n; i++)
scanf("%d %d",&x[i],&y[i]);
Вычисляем и выводим площадь многоугольника.
printf("%.3lf\n",findArea(x,y));
Реализация алгоритма – формула
Сюрвейера
#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;
double
findArea(vector<int> &x, vector<int> &y)
{
double s = 0;
x.push_back(x[0]); y.push_back(y[0]);
for(int i = 0; i < x.size() - 1; i++)
s += y[i+1] * x[i] - y[i] * x[i+1];
return
fabs(s) / 2.0;
}
vector<int> x, y;
int i, n,
a, b;
int main(void)
{
scanf("%d",&n);
for(i = 0; i
< n; i++)
{
scanf("%d
%d",&a,&b);
x.push_back(a);
y.push_back(b);
}
printf("%.3lf\n",findArea(x,y));
return 0;
}
Реализация алгоритма – классы
#include <stdio.h>
class Point
{
private:
double x, y;
public:
Point(double x = 0, double
y = 0) : x(x), y(y) {};
double GetX()
{
return x;
}
double GetY()
{
return y;
}
// cross product
double operator* (const Point &p)
{
return this->x *
p.y - this->y * p.x;
}
};
class Shape
{
protected:
Point *p;
int size;
public:
Shape(int size = 0) : size(size)
{
p = new Point[size+1];
}
~Shape()
{
delete[] p;
}
};
class Polygon : public
Shape
{
public:
Polygon(int n = 0) : Shape(n)
{};
void ReadPoints(void)
{
double x, y;
for(int i = 0; i <
size; i++)
{
scanf("%lf %lf",&x,&y);
p[i] =
Point(x,y);
}
p[size] = p[0];
}
double Area(void)
{
double s = 0;
for(int i = 0; i <
size; i++)
s += p[i] *
p[i+1];
return (s < 0) ? -s/2 : s/2;
}
};
int n;
int main(void)
{
scanf("%d",&n);
Polygon p(n);
p.ReadPoints();
printf("%.3lf\n",p.Area());
return 0;
}